【C4D】半正/阿基米德多面体

半正多面体（semiregular solid）也称为“阿基米德多面体”（Archimedean solid），它是由两种以上正多边形组成且所有顶点都等价的凸多面体。阿基米德多面体共有13种，比如常见的C60（足球烯）就是其中的一种——截角二十面体。由于所有顶点等价，可以用每个顶点处的正多边形排列来定义多面体的名称。例如，截角二十面体的每个顶点由1个正五边形和2个正六边形共享，所以可定义为5·6·6（一般按照顺时针顺序，边数尽可能由小到大排列）。

所有的13个阿基米德多面体均可通过基本的柏拉图多面体（Platonic solid，即正多面体）得到，最简单地，直接对正多面体的顶点进行截断就能得到相应的截角多面体。在Cinema 4D软件中，可以对宝石体（Platonic）对象进行倒角（bevel），倒角的“构成模式”选择点，“偏移模式”选择按比例，“偏移”百分比为33.333%。

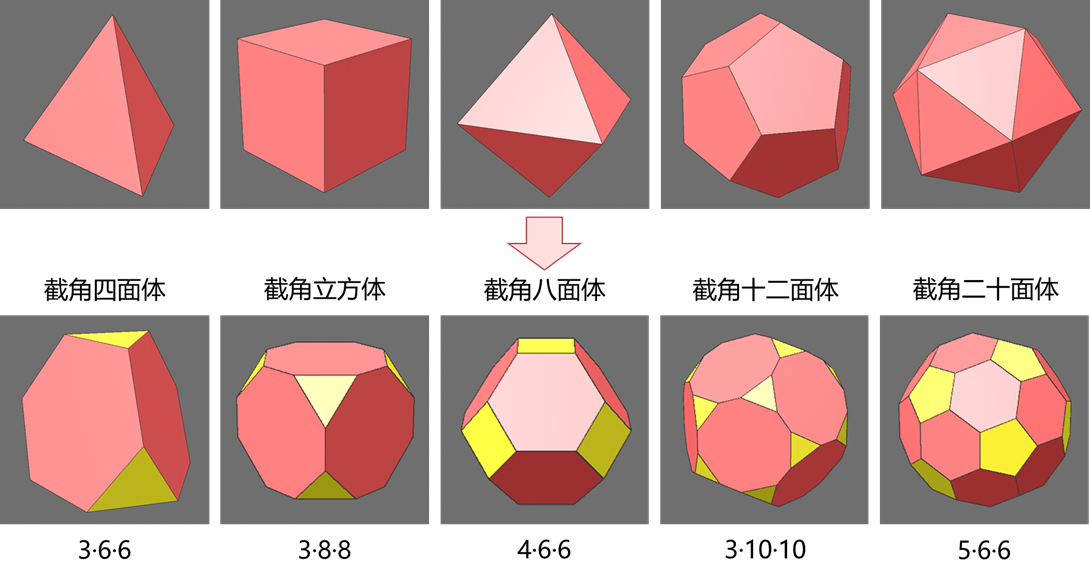
以上都是顶点部分截断的情形，如果是完全截断（点倒角“偏移”百分比为50%），将得到另外两种新的阿基米德多面体——立方八面体（cuboctahedron）和截半二十面体（icosidodecahedron）。由于立方体和正八面体互为对偶多面体，所以它们的顶点完全截断得到的都是立方八面体。同理，正十二面体和正二十面体也互为对偶多面体，它们的顶点完全截断得到的都是截半二十面体。比较特殊的是正四面体，它的顶点完全截断将得到正八面体。

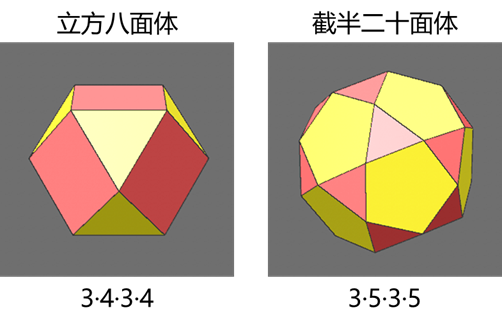
除了对点倒角之外，倒角的“构成模式”还可以选择边，这种情况下又可以得到两种新的多面体——小斜方截半立方体（rhombicuboctahedron）和小斜方截半二十面体（rhombicosidodecahedron）。同样，我们只对立方体和正二十面体操作就能分别得到。这里需要注意的是倒角“偏移”百分比，对于立方体，百分比为1/(2+sqrt(2))（约为29.289%）；对于二十面体，百分比为3/(7+sqrt(5))（约为32.481%）。

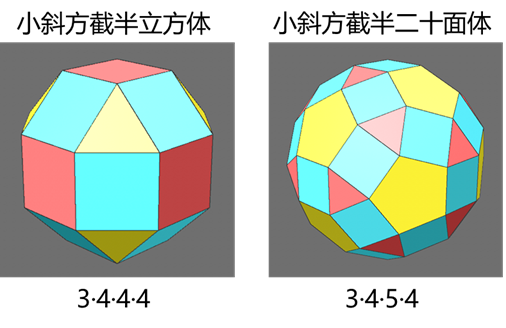
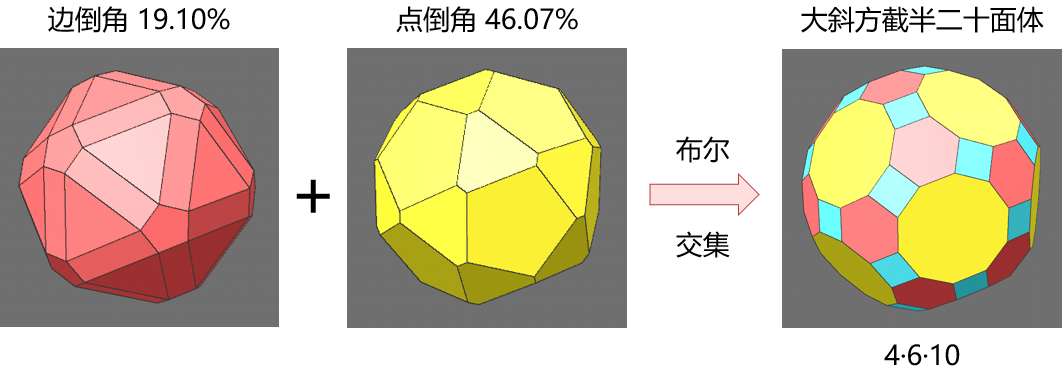
与小斜方相对应的是大斜方截半立方体（truncated cuboctahedron）和大斜方截半二十面体（truncated icosidodecahedron），这两种多面体的创建过程稍微复杂一些。如果直接在立方八面体或截半二十面体的基础上进行点倒角，最后得到的多边形面将不是正多边形。这里可以采用布尔求交集的方法，以大斜方截半立方体为例，分别对两个等大立方体的点和边进行倒角，边的倒角“偏移”百分比为1/(4+sqrt(2))（约为18.47%），点的倒角“偏移”百分比是其三倍（约55.41%）。由于点的倒角值超过了50%，模型的边有穿插，布尔交集运算后可能得不到完整的多面体，需要用多边形画笔工具补全缺少的面。另一个大斜方截半二十面体采用同样的方法创建，边的倒角“偏移”百分比为1/(3+sqrt(5))（约为19.098%），点的倒角“偏移”百分比为(5-sqrt(5))/6（约为46.0655%）。

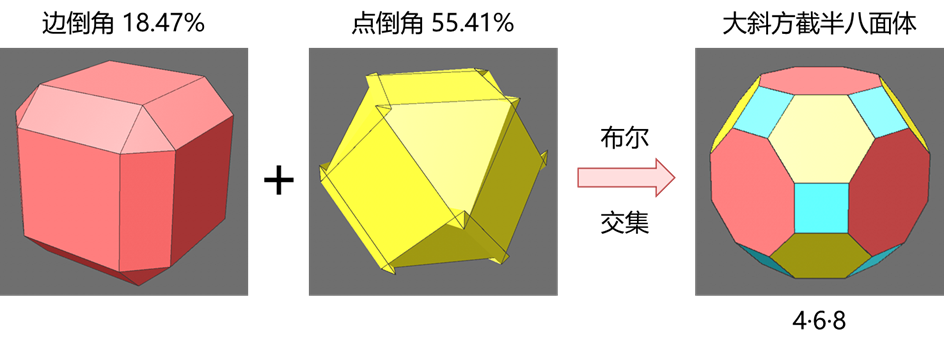
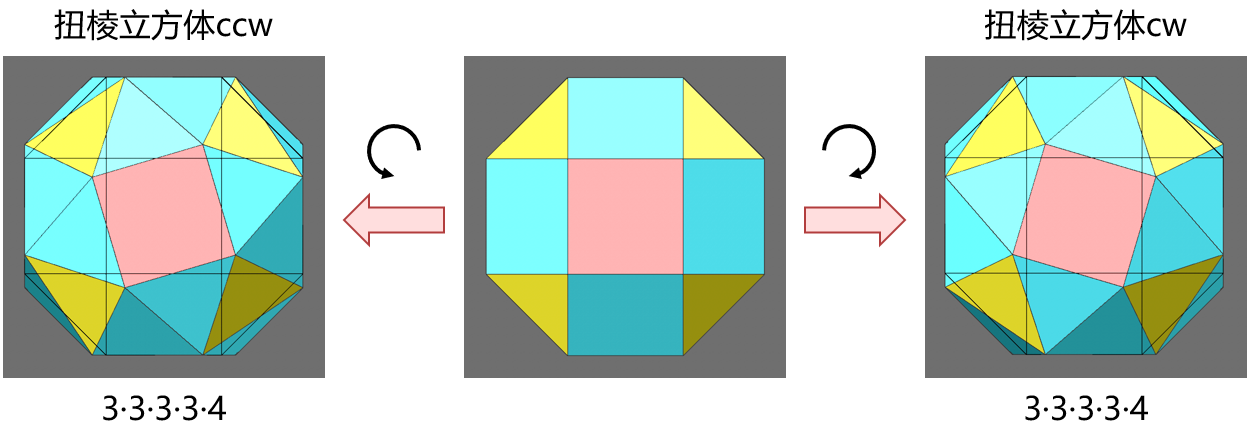
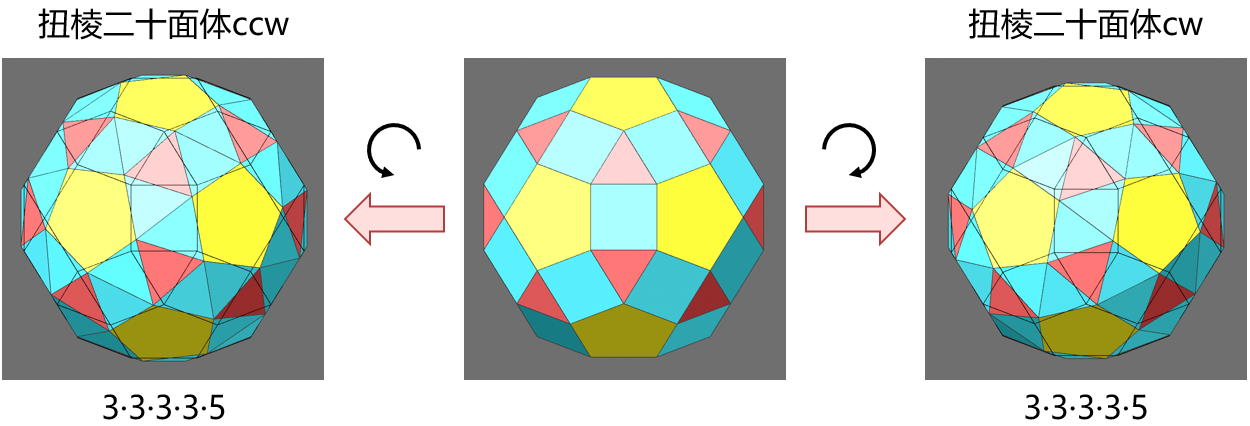
最后两种特殊的阿基米德多面体是扭棱立方体（snub cube）和扭棱二十面体（snub dodecahedron），每种都有两种手性对称的变体。扭棱多面体可以通过旋转小斜方截半立方体（或小斜方截半二十面体）中呈立方体（或二十面体）对称性的正多边形面得到，根据旋转方向的不同，可得到顺时针（cw）和逆时针（ccw）两种手性造型。关于扭转的角度计算非常复杂（可参考这里），例如小斜方截半立方体中，呈立方体对称性的六个面顺时针或逆时针旋转16.4675°，即可得到扭棱立方体（扭转变形的四边面拆分为两个三角面）。从小斜方截半二十面体到扭棱十二面体的扭曲角约为13.5°（近似值，未找到详细数值）。

参考文件下载：阿基米德多面体.c4d